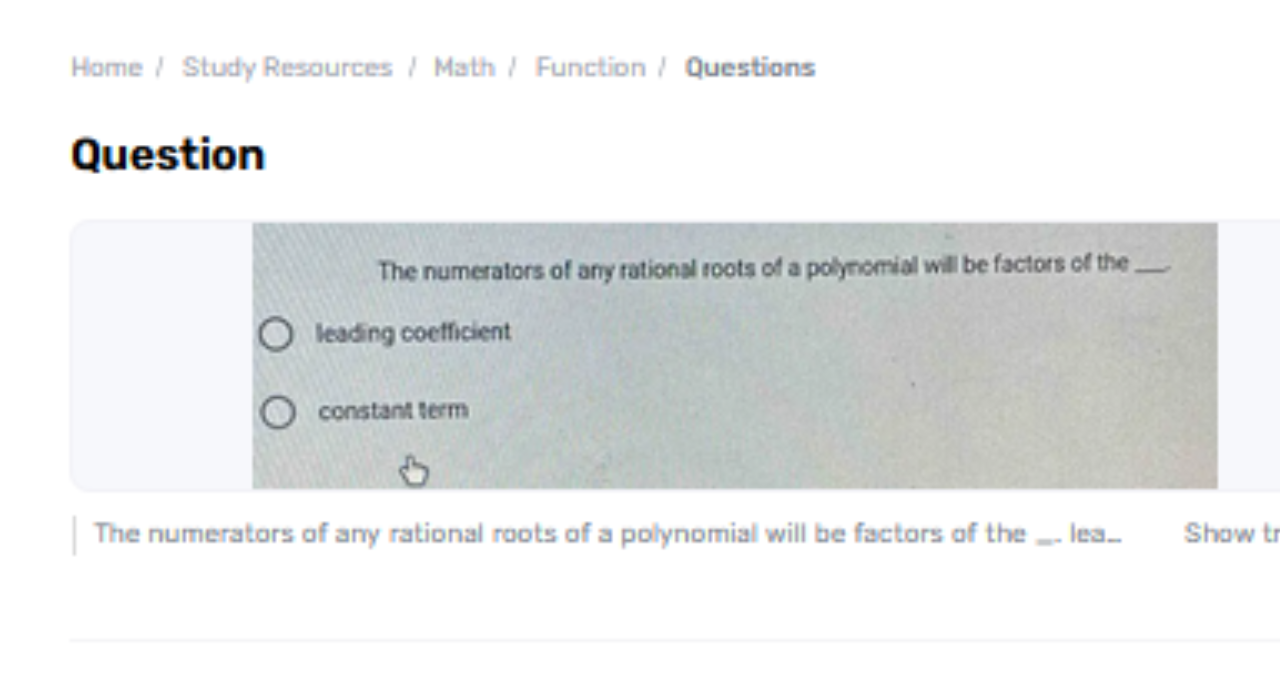
In polynomial math, especially in polynomial conditions, deciding the roots of a polynomial is significant for understanding its behavior and arrangements. For polynomials with numbers coefficients, the Sound Root Hypothesis may be a profitable apparatus, the numerators of any rational roots of a polynomial will be the factors of the ___ term. This hypothesis gives a way to recognize potential levelheaded roots of a polynomial by relating them to the coefficients of the polynomial.
A key perspective of this hypothesis includes understanding the relationship between the numerators of the levelheaded roots and the polynomial's terms. This exposition investigates the Judicious Root Hypothesis, centering on the truth that the numerators of any judicious roots of a polynomial are variables of the steady term.
Variables of the Steady Term and Judicious Roots
The numerators of any sound roots of a polynomial with numbers coefficients are variables of the steady term. This guideline, determined from the Judicious Root Hypothesis, guarantees that as it were those numerators that isolate the steady term can be potential judicious roots. This understanding makes a difference in effectively distinguishing conceivable levelheaded arrangements from polynomial conditions.
The Sound Root Hypothesis
The Judicious Root Hypothesis states that any levelheaded root of a polynomial equation with numbers coefficients can be expressed within the shape pqfrac{p}{q}qp, where I may be a calculation of the steady term and I could be a figure of the driving coefficient. This hypothesis is instrumental in testing potential roots by giving an organized strategy for recognizing conceivable judicious arrangements. To get why the numerators of the levelheaded roots are components of the steady term, we must dive into the structure of polynomial conditions and the theorem's suggestions.
Distinguishing Potential Roots
Where ana_nan is the driving coefficient and a0a_0a0 is the consistent term. Concurring to the Levelheaded Root Theorem, in case a judicious number pqfrac{p}{q}qp could be a root of the polynomial, at that point I must be a figure of the steady term a0a_0a0. Typically when substituting pqfrac{p}{q}qp into the polynomial and setting it to rise to zero, the term including Q must cancel out, clearing out as it were the terms including pp. Hence, I must partition a0a_0a0 for the condition to be fulfilled.
Down to earth Application
In common terms, the Sound Root Hypothesis disentangles the method of finding sound roots by narrowing down the conceivable candidates. By posting all components of the steady term a0a_0a0 and testing these as potential numerators of the sound roots, one can effectively distinguish valid roots of the polynomial. This strategy is especially valuable when tackling polynomial conditions where trial and blunder might something else to be unreasonable due to the polynomial's complexity or degree.
Key Steps for Using the Gauth App to Reply to an Inquiry
1. Download and Enlist
Get the Gauth app from your app store and complete the enrollment preparation.
2. Sign In
Open the app and log in along with your client qualifications.
3. Find the Question
Utilize the look work or browse to locate the address you want to reply.
4. Provide Your Reply
Enter your reaction within the assigned zone and yield it for thought.
Conclusion
In conclusion, the Judicious Root Hypothesis gives an orderly approach to finding judicious roots of polynomials with numbers coefficients. Concurring with this hypothesis, the numerators of any levelheaded roots must be factors of the steady term of the polynomial. This relationship helps in narrowing down potential roots and disentangles the method of fathoming polynomial conditions. Understanding and applying this hypothesis viably is significant for logarithmic problem-solving and polynomial examination.